What is Problem Solving?1
Problem solving is the approach of gathering information and using logical reasoning to solve problems in a given scenario.
In problem solving, three distinct skills are necessary to be effective:
- knowledge of basic arithmetic;
- knowing how to incorporate them in new contexts; and
- knowing how to apply it.
Most occupations need good problem solving skills. Architects and engineers for example must solve complex problems in designing and constructing modern buildings.
To be a proficient problem solver, knowledge of numbers and fractions should not be the end, one must be able to explore and reinterpret information and knowledge to be used in different contexts.
Types of Reasoning
Inductive2
Inductive reasoning implies the formulation of conclusions based on the observation of examples.
The conclusions made from inductive reasoning are called conjectures[^conjectures].
Deductive3
Deductive reasoning is the process of reaching conclusions through the application of established principles, assumptions, or procedures.
Counterexamples[^counterexamples]
In mathematical reasoning, we often use examples to prove things are true or not. In problem solving, we use inductive or deductive reasoning to determine this.
In some cases, it is easier to determine something is false rather than true, therefor we use counterexamples.
Counterexamples are logical tools that determines truth by finding a case where a statement can be false.
For example, if someone said:
“All dogs are good”
And you respond with:
“My cat is good, therefor he is a dog”
Since your cat cannot be a dog, you then disprove the first statement using the second statement as a counterexample.
Logic Puzzles
There are three dominant logical puzzles that are used to practice problem solving skills.
They are the following:
- Deduction puzzles
- Kenken puzzles
Deduction puzzles4
These are puzzles that involve a grid relationship between two sets of things.
In a puzzle, there are given statements that gives direct and indirect answers to the relationship of the two sets.
Below is an example:
- Maria gets home from work after the banker but before the dentist
- Sarah, who is the last to get home from work, is not the editor.
- The dentist and Sarah leave work at the same time.
- The banker lives next door to Brian.
| Editor | Banker | Chef | Dentist | |
|---|---|---|---|---|
| Sean | ||||
| Maria | ||||
| Sarah | ||||
| Brian |
Kenken puzzles5
Kenken puzzles are a modification of sudoku where numbers in a vertical and a straight line cannot repeat.
The key difference in kenken puzzles is that areas are defined by an arithmetic operation.
Below is an example:
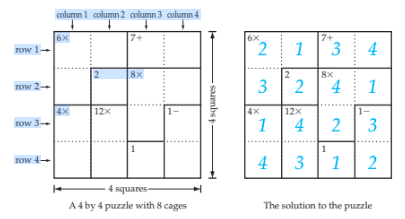
Mathematical Logic Problems
Sequence6
Some sequences may appear to be a random series, but upon solving, the sequence is revealed to be a nested series of sequences.
Below is an example:
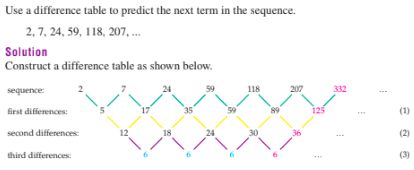
Nth-Term7 of a Sequence8
In some cases, you might be given a series of shapes that change in size as the grow in term ().
To reveal and solve for the underlying pattern of the sequence, it useful to determine how that sequence of shapes grows.
In the example below:
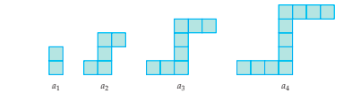
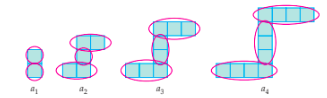
We can notice that the tail and heads grow with the term, and the body grows with 1 subtracted from the term.
That gives us this formula: Some useful things to note for solving this:
- If you notice a consistent square shape in the sequence, it is a square of a number ().
- If you notice that a number is consistently the same as the term, then they are equal ().
- If you notice a number is multiple of a term, then it is ().
- If you notice a number is consistently the same distance away from your term, then it is a sum or difference of your term an a number ().
Polya’s Problem Solving Strategy9
George Polya created a four step problem solving strategy that is deceptively simple; meaning it looks simple but can be expanded into complicated but manageable levels.
His strategy is comprised of the following:
- Understand the problem.
- Devise a plan.
- Carry out the plan.
- Review the solution.
Footnotes
-
Problem solving is the approach of using logical reasoning in solving problems; involves the application of basic arithmetic in new contexts. ↩
-
Inductive reasoning is the process of concluding based on an observation of examples. ↩
-
Deductive reasoning is the use of established rules and ideas to make conclusions. ↩
-
Deduction puzzles utilize deductive reasonings to identify the true values in the puzzle; commonly the identities of characters. ↩
-
Kenken puzzles are a modification of sudoku that utilizes areas defined by arithmetic operations as clues. ↩
-
Sequences may seem random but may be a series of nested series. ↩
-
The nth term is a number of the term in a sequence. ↩
-
Nth-term sequences are patterns that have an underlying formula that is dependent on an nth term. ↩
-
The Strategy made by George Polya involves four steps for solving problems. ↩