Sets of Numbers

Basic Properties of Sets

Sets are an attempt to better understand the world around us; we humans have a knack and preference for classifying similar objects in the same group. Astronomers saw related stars and deemed them part of the same constellations, zoologists saw related animals and deemed them parts of the same family, and etc.

Sets can be designated with two methods:

1. describe the set using words; or
2. write down every member between two curly braces ( $\left\{\dots \right\}$ ), otherwise known as the Roster Method.

Method 1 can be done by simply describing the contents of your set. Some examples of this are:

• The set of all even numbers.
• The set of all negative numbers.
• The set of all number divisible by 5.

Basic Number Sets

There are a basic set of numbers and they are often represented by a specific letter written in blackboard bold ( $\mathbb{A},\mathbb{B},\mathbb{C}\dots$ ).

Natural or Counting Number - $\mathbb{N}=\{1,2,3,\dots \}$

Whole Numbers - $\mathbb{W}=\{0,1,2,\dots \}$

Integers - $\mathbb{Z}=\{\dots ,-1,0,1\dots \}$

Rational Numbers - $\mathbb{Q}=\text{the set of all terminating or repeating decimals}$

Irrational Numbers - $\mathbb{I}=\text{the set of all nonterminating, nonrepeating decimals}$

Real Numbers - $\mathbb{R}=\text{the set of all rational and irrational numbers}$

Definition Regarding Sets

A set is well defined if it is possible to determine whether any given item is an element of the set. The set of all letters in the english alphabet is an example of a well defined set because you can easily define its members, whereas the set of all great songs is not a well defined set because it has no standard method to identify its members.

To write in the mathematical language that the number 4 is a natural number, we would write the following:

$4\in \mathbb{N}$

To write that an element is not a member of the set, we would write the following:

$-1\notin \mathbb{N}$

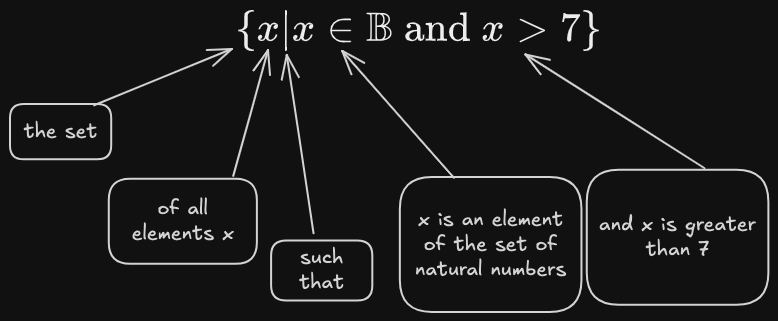
Set Builder Notation

Another way to performing method 1 is to use the mathematical language in a the set builder notation.

An example of a set made with set builder notation is the following:

$\{x|x\in \mathbb{N}\text{ and }x>7\}$

The breakdown for the parts of this expression is the following:

Universal Sets and the Complement of a Set

There exists a set that contains all possible values called the universal set ( denoted as $\mathbb{U}$ ). The opposite of the universal set is the null set ( denoted as $\varnothing$ or $\{\}$ ) and is a set containing nothing.

A complementary set is simply all elements that a particular set needs to become equal to the universal set.

Complementary sets are denoted with prime notation ( ex. the complementary set of set $A$ is $A^{\prime }$ ).

With this definition for complementary set, we can say that the complementary set of the universal set is a null set.

${\mathbb{U}}^{\prime }=\varnothing$

Subsets

Subsets are sets that are found within another set, this relationship is denoted using the subset operator ( $\subseteq$ ).

If we have a set $A$ and $B$ with the following values:

$A=\{1,2,3,4,5\}\text{ and }B=\{2,4\}$

Then we can say that the set $B$ is a subset of set $A$.

$B\subseteq A$

The Number of Subsets of a Set

To calculate the number of subsets in a set, count the number of elements in that set and raise 2 to that power.

OP

The Number of Subsets in a Set

• Use case:
  • When calculating the number of subsets in a set
• Variables:
  • $|A|$ - Number of elements in a set
• Formula: $\text{Number of subsets}=2^{|A|}$

Link to original

Set Operations

Sets–– just like any other object in mathematics ––can have operations done with or on them. Just like conventional Arithmetic, Set operations use mostly binary operations ( needs two arguments or values ).

Intersection

An intersection represent a set that contains all elements that is present in both sets.

An intersection is expressed as such:

$A\cap B$

and can be visualized as the following:

Disjoint Sets

A special type of intersection where no elements are present in both sets; in other words, the operation is equal to a null set.

$A\cap B=\varnothing$

Union of Sets

A union of sets is an operation that returns a set that contains all of the elements between the two given sets.

This is how to express a union:

$A\cup B$

This is how to illustrate a union:

Equality and Equivalence of Sets

Equality is a concept we are all familiar with and will continue to be familiar with because it is also present in the field of Set Theory.

Equality is means that both elements involved are one to one with one another and share no differences in value.

$\{A,B,C,D\}=\{A,B,C,D\}$

In set theory, besides equality, we have the equivalence operator, which illustrates that both sets share the same number of elements.

$\{A,B,C\}\backsim \{\alpha ,\beta ,\kappa \}$

Application of Sets

The concept of sets can be applied in counting problems where a set is divided into different demographics where some elements are members of both demographics.

Lets have the following as an example:

A movie company is making plans for future movies it wishes to produce. The company has done a random survey of 1000 people, the results of the survey are shown below:

• 695 people like action adventures.
• 340 people like comedies.
• 180 people like both action adventures and comedies. Of the people surveyed, how many people

1. like action action adventures but not comedian?
2. like comedies but not action adventures?
3. do not like either of these types of moves?

To answer the aforementioned questions

1. we must first visualize all the sets involved.

In the visualization above, we made a box labeled $U$ which represents our universal set containing all 1000 of our survey participants. Within the universal set are two sets $A$ and $B$ which represents the set of survey participants who like action adventure movies and comedies respectively.

2. Next, using our given survey data, we should label each area with their respective numbers, starting with the part that is deeply intersected–– in this case, the area in between set $A$ and $B$.

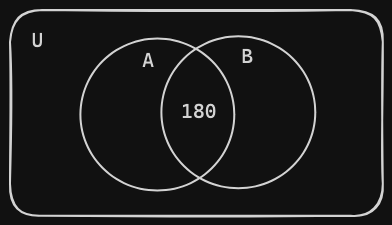
In the visualizations above, we labeled the intersection of set $A$ and $B$ with the number 180 from our given sets of data. The intersection represents elements–– in this case, survey participants that are in both sets $A$ and $B$ ( they like both genres ).

3. Next, we do the same as step 2, but with the next remaining areas, which are the remaining areas of sets $A$ and $B$.

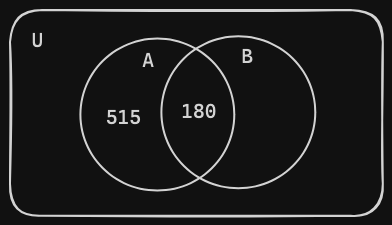
In the visualization above, we labeled the remaining area of set $A$ with the number 515 because the data of survey participants who liked action movies was 695 and we already accounted for 180 of those individuals, therefor the members of set $A$ is equal to $695-180=515$.

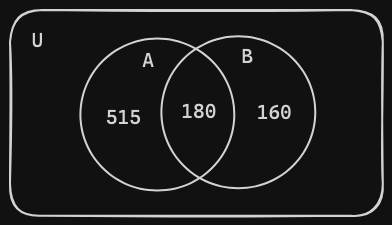
In the visualization above, we did the same as the last step with set $B$, the value’s equation is as follows: $340-180=160$.

4. Now that the remaining area is only the universal set’s, we can calculate its number of members by summing up all the numbers we had labeled onto our set and subtracting that from the total 1000 survey participants ( since the universal set accounts for all survey participants ). The equation is as follows: $1000-(515+180+160)=145$

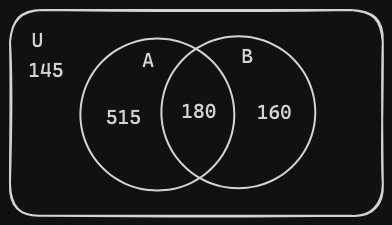
5. Now with all our values known, let’s answer our questions.
   1. like action action adventures but not comedian? 515 people
   2. like comedies but not action adventures? 160 people
   3. do not like either of these types of moves? 145 people